Batch Normalization은 2015년 arXiv에 발표된 후 ICML 2015에 게재된 아래 논문에서 나온 개념입니다.
"Batch Normalization: Accelerating Deep Network Training b y Reducing Internal Covariate Shift"
https://arxiv.org/pdf/1502.03167.pdf
현대 딥러닝 아키텍처에서 학습 속도(training speed)를 비약적으로 향상시킬 수 있었던 방법 중 하나인 배치 정규화(Batch Normalization)에 대한 설명을 해보겠습니다!
Paper에 대한 real review는 아니지만, 참고 학습 영상(https://youtu.be/m61OSJfxL0U)을 학습하며 스스로 이해시켰던 방법으로 설명해보겠습니다!
목차
Batch Normalization 동작설명(Training)

먼저 Batch Normalization을 왜 하는 것인지, 그리고 이것이 왜 잘 작동하는 것인지에 대해서 설명을 해보겠습니다.
해당 그림을 보시면 기본적인 Neural Network구조를 보실 수 있습니다.
구조를 설명하자면 입력에서부터 네트워크를 지나면서 통과하다가 Weight들이 Sum 되고 활성 함수를 지나면서 값을 도출합니다.
이 논문의 취지는 활성함수를 지나기 전 weight들이 sum 되어서 들어오는 값들을 잘 좀 만져보자 라는 것에 있습니다.
예를 들어 mini-batch의 개수가 32개라고 했을 때, 한 노드에 대해서 32개의 입력 값들이 들어오게 됩니다.

예를들어 mini-batch의 개수가 32개라고 했을 때, 한 노드에 대해서 32개의 입력 값들이 들어오게 됩니다.
이 값들의 평균, 분산을 구하고 Normalize를 합니다.
논문에서는 분산에다가 ε(EPSILON) 값을 더해줬습니다. 이유는 표준편차가 0일 경우를 대비하기 위해서라고 합니다.
Xi는 32개의 각각 값들입니다. Xi를 그들의 평균으로 빼고, 그들의 분산으로 나누게 되면
이것은 평균이 0, 분산이 1인 분포를 따르게 됩니다.
Normalize 된 값에 γ(gamma)를 곱하고 β(beta)를 더하게 되면 결괏값이 나옵니다.
이것이 Batch Normalization의 전반적인 구조입니다.
다시 말해서, mini-batch의 개수가 32개라고 했을 때, 32개의 Data를 다 통과시키고 그들의 평균과 분산을 구해서 normalize 하고 그 도출된 값에 γ(gamma)를 곱하고 β(beta)를 더하게 된 것이 Batch Normalization의 결과입니다.
그렇다면 γ(gamma)와 β(beta)를 어떻게 구할까를 생각해야 합니다.
그 방법은 γ(gamma)와 β(beta)도 Training parameter에 포함을 시킵니다.
따라서, Weight처럼 γ(gamma)와 β(beta)도 Training 합니다.
각 노드당 2개씩을 새롭게 Training 할 parameter를 추가하는 겁니다. Weight가 늘어난 셈이죠.
Batch Normalization 동작 설명(Test)
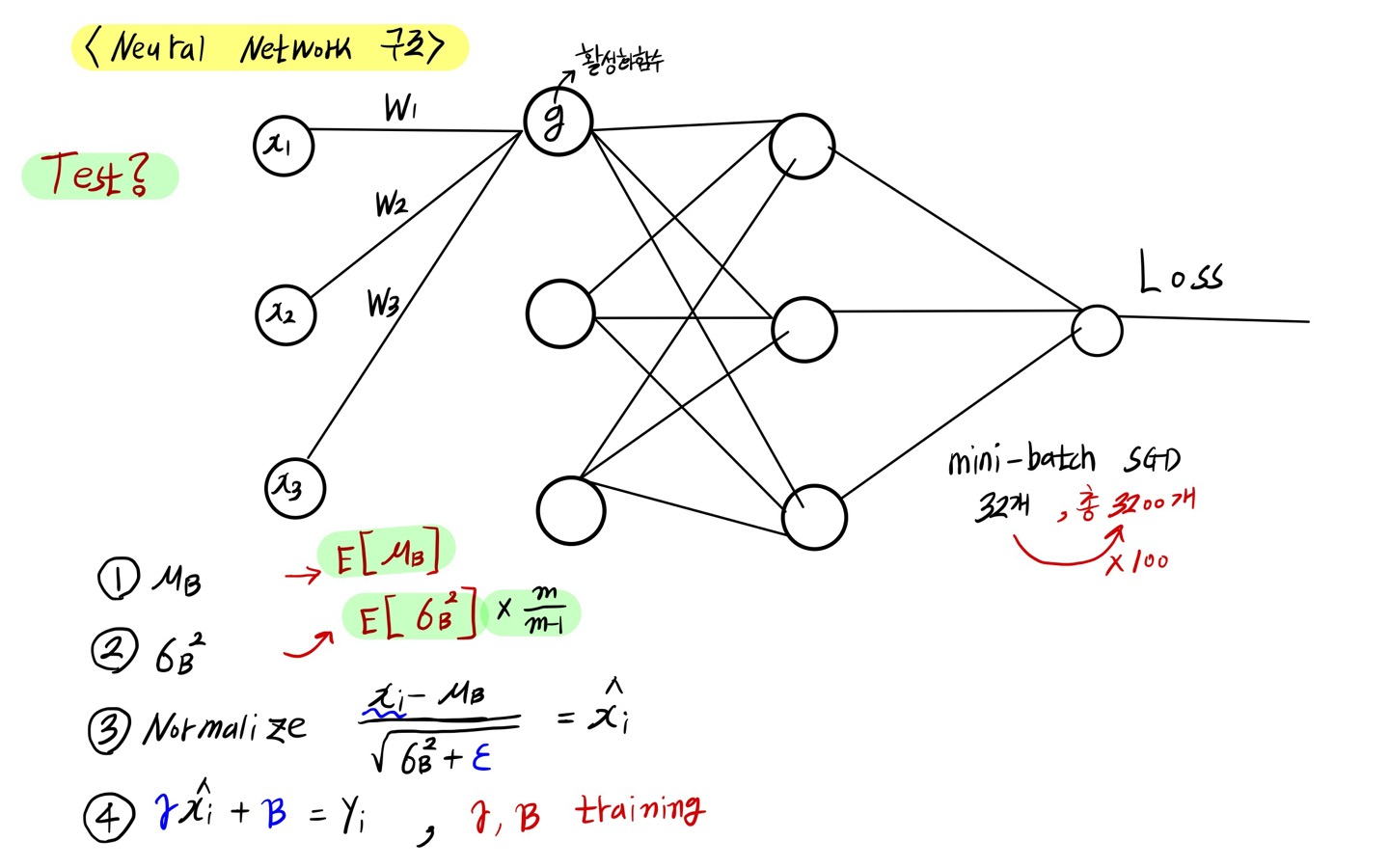
사실 mini-batch라는 것은 Training 할 때에만 쓰이는 존재입니다.
Test를 할 때 32개 값을 넣어서 진행하진 않겠죠
그렇다면 Test는 하나씩 넣어서 결괏값을 봐야 하는데 어떻게 진행할 것인지에 대해서 생각을 해봐야 합니다.
그래서 Batch Normalization에서는 아래와 같은 해답을 제시했습니다.
총 Data가 3200개라고 했을 때, mini-batch가 32개라면 총 100번의 과정이 이루어집니다.
그렇다면 총 100번의 평균과 분산이 계산이 되었으니 그 100번의 표본 평균의 평균과, 표본 분산의 평균을 계산해서 Test에 사용을 하자라는 것입니다.
그 도출된 값을 이용해서 Normalize 하고, 그다음에는 Training 과정에서 얻어낸 γ(gamma)를 곱하고 β(beta)를 더해줌으로써 값을 도출합니다.
Test 할 때는 분산에 m/(m-1)을 곱한다.
해당 그림을 보시면 표본 분산의 평균값에 m/(m-1)이 곱해져 있는 것을 볼 수 있습니다.
수학적인 계산을 해보시면 표본 분산의 평균값은 모 분산으로 가지 않기 때문에 모분산으로 가기 위해서는 m/(m-1)을 곱해준다고 합니다.
Test에서 E(평균)은 moving average 방법으로..!
논문에서는 Test과정에서 표본 평균의 평균과 표본 분산의 평균을 구할 때 Moving average 방법을 이용한다라고 나와있습니다. Moving average의 종류는 많습니다. 해당 논문에서는 구체적으로 어떤 Moving average를 사용했는지는 안 나와있지만, 많은 리뷰글에서 Exponential moving average방법을 사용했다라고 추측합니다.
이 방법은 평균을 취할 때 과거의 것들은 Weight를 적게 주고, 최근의 것들은 Weight를 많이 줘서 평균을 구하는 방법이라고 합니다.
예를 들어, 총 3200개의 Data를 학습시킨다고 했을 때 처음에는 Weight들이 안정이 되기 전이니까 초반의 값들은 굉장히 안 좋은 값들이 나오겠죠.
그래서 좀 Weight들이 안정이 되고 나서의 mini-batch들의 대한 평균을 구하는 것이 값을 내기에 더 나을 겁니다.
따라서, 해당 논문에서는 Moving average 방법을 통해 이 문제를 해결해 줄 수가 있다고 했습니다.
BN을 직관적으로 생각해보자

①~④ 과정들을 다시 한번 살펴봐봅시다.
사실 이 과정들은 그냥 빼고, 나누고, 다시 곱하고 더한 과정입니다.
이런 수식적인 과정들은 Weight들과 Bias들로 충분히 할 수 있는 일입니다.
(▶ 위 그림 왼쪽 상단 수식 참고)
그래서 저는 여기서 ①~④ 과정들을 굳이 왜 해야 하나?라는 의구심이 들었습니다.
어떻게 Vanishinig Gradient(기울기 소실) 문제를 막을까?
Batch Normalization의 핵심은 Nomalize 한 다음에 ④ 과정을 통해 다시 뿌려줬다는 게 핵심인데,
이게 왜 의미가 있는지 생각해봅시다.
▶ 위 그림 우측 하단 그래프 참고
직관적으로 이 Random variable들을 모래 알갱이라고 생각했을 때, 32개의 알갱이가 퍼져있을 겁니다.
이 알갱이들을 Normalize 했다는 것은 두 그래프 중 왼쪽 모양처럼 평균이 0이고 분산이 1인 분포를 가지도록 모아줬다는 의미겠죠.
그다음에 ④ 과정에서 γ(gamma)를 곱하고 β(beta)를 더하는 과정을 지나게 되면 두 그래프 중 오른쪽 모양처럼 새롭게 다시 뿌려주는 겁니다. 다시 뿌려주는 게 무슨 의미일까요?
Sigmoid라는 활성 함수 지날 때를 생각해봅시다.
만약에 Normalization이 없었다면 입력값들이 미분 0에 가까운 곳에 모여있을 수가 있습니다.
미분이 0이 된다면 Vanishing gradient문제가 발생하기 때문에, normalize를 통해 중심으로 모이도록 해서 기울기를 살아나게 해 줄 수 있습니다. 이 과정을 통해 Vanishing gradient 문제를 어느 정도 해결할 수 있겠죠.
그러나 중심으로 모이게 하는 것이 좋다면, ①~③과정까지 하면 되지 않을까?라는 생각을 하게 됩니다.
논문에서도 이러한 생각을 하였지만, ④ 과정을 진행하지 않으면 문제가 생긴다는 사실을 알게 되었습니다.
값이 Sigmoid함수의 중심에 가까운 곳에만 집중되다 보니 비선형적인 함수의 꼴이 아니게 돼버렸습니다.
비선형적인 모델이 되어버린다면 Neural Network의 성립 자체가 불가능 해집니다.
이 문제를 해결하기 위해서 ④번 과정으로 γ(gamma), β(beta)를 training 하여 조정함으로써 적절한 곳에 값을 뿌릴 수 있는 것입니다.
왜 Learning rate를 키워도 될까?
④번 과정을 하게 되면, 입력 값들에 대한 update를 해야 하는 편차들이 크지 않아서 learning rate를 크게 해도 상관이 없다고 논문에 나와있습니다.
결론적으로 이 논문에서 주장하는 바로는 정확도에 수렴하는 과정이 Batch Nomalization을 사용했을 때가 14배나 빨랐다고 합니다.
또한 Batch Normalization을 사용했을 때 기울기 소실 문제를 해결하고, learning rate를 키울 수 있고, Drop out을 하지 않아도 된다는 장점이 있습니다.
'Main > Paper Review' 카테고리의 다른 글
| [Paper Review] MobileNet V1 (0) | 2022.05.26 |
|---|---|
| [Paper Review] SENet: Squeeze-and-Excitation Networks (0) | 2022.05.16 |
| [CNN-Algorithm] ResNet (0) | 2022.03.22 |
| [CNN-Algorithm] GoogLeNet(Inception) (0) | 2022.03.21 |
| [CNN-Algorithm] VGGNet (0) | 2022.03.21 |




댓글