본 내용은 김성훈 교수님의 '모두를 위한 딥러닝' 강의와
https://pythonkim.tistory.com/notice/25 를 참고하여 제작하였습니다.
이 알고리즘은 Classification 알고리즘 중에서 굉장히 정확도가 높은 알고리즘으로 알려져 있습니다.
Logistic (Regression) Classification 알고리즘을 잘 학습한다면, 이 강좌의 목표인 Neural Network와 Deep learning을 잘 이해하기에 다가갈 수 있을 것입니다.
목차
1. Logistic Classification의 가설 함수 정의

두 가지 분류를 활용할 수 있는 몇 가지 예제를 설명하고 있습니다. 스팸 메일 탐지, 페이스북 피드 표시, 신용카드 부정 사용은 두 가지 값 중의 하나를 선택하게 됩니다. 프로그래밍에서는 이 값을 boolean이라고 부르지만, 여기서는 쉽게 1과 0으로 구분합니다. 1은 spam, show, fraud에 해당한다. 1과 0에 특별한 값을 할당하도록 정해진 것은 아닙니다. 다만 찾고자 하는 것에 1을 붙이는 것이 일반적입니다.
1.1 Linear Regression을 Classification에 사용할 때 발생할 수 있는 문제

이번 그래프에서는 학생들의 성적의 모든 점수를 0 또는 1로 변환했다는 것을 전제로 합니다.
Linear regression은 Wx+b 공식을 통해서 직선을 긋고 이걸 토대로 결과를 예측하는 방식입니다.
교수님께서는 기존 그래프에 공부를 많이 한 학생이 등장하면 기울기가 달라지기 때문에 문제가 발생한다고 말씀하셨습니다.

Linear Regression을 Classification에 사용할 때 발생할 수 있는 문제에 대해서는 앞에서 설명했습니다.
Wx+b라는 공식을 있는 그대로 사용하면 W를 1/2이라고 했을 때, x의 값이 100인 경우 50이라는 엄청난 값이 만들어질 수 있습니다.
0과 1만을 사용해야 하는데, 범위를 벗어나는 값이 나오게 됩니다. 50보다 작으면 0, 크면 1이라고 표현하거나 1/2보다 작으면 0, 크면 1이라고 표현할 수 있는 추가 코드가 반드시 있어야 합니다.
아래 그림에서는 이러한 표현식을 sigmoid라고 설명하고 있습니다.
1.2 Sigmoid function(시그모이드 함수)

Sigmoid function(시그모이드 함수)는 앞에서 배운 공식(Wx + b )이 만들어 내는 값을 0과 1 사이의 값으로 변환합니다. 어떤 값이든지 sigmoid 함수를 통과하기만 하면 0과 1 사이의 값이 되는 놀라운 기적을 보여줍니다.
왼쪽 그림의 공식에 해당 조건들을 만족해보면 오른쪽 그래프처럼 그려진다는 것을 알 수 있습니다.
1. e로 시작하는 계산식이 0일 때, 1/1이 되어서 최댓값인 1이 된다.
2. e로 시작하는 계산식이 매우 클 때, (1/큰 수)이 되어서 최솟값인 0이 된다.
3. WX가 0일 때, 지수가 0이 되어, 분모는 2가 되고, 이때 중간값인 1/2이 된다.
Sigmoid 함수는 아주 중요하니까, 다시 한번 강조합니다.
Sigmoid는 Linear Regression에서 가져온 값을 0과 1 사이의 값으로 변환한다. z가 0일 때, 0.5가 된다.
2. Logistic Regression의 cost 함수 설명
2.1 Cost function

Linear Regression에서 배운 hypothesis와 이번에 배운 hypothesis를 비교해서 보여주고 있습니다.
hypothesis는 cost 함수를 구성하는 핵심이기 때문에, 여기서는 cost 함수 또한 이전과 달라져야 한다고 얘기하고 있습니다.
그림의 왼쪽 부분은 매끈한 밥그릇이고, 오른쪽 부분은 울퉁불퉁합니다.
김성훈 교수님은 sigmoid 모양에 대해서 e의 지수 형태의 그래프를 사용했기 때문에 구부러진 곡선이 연결된 느낌입니다.
울퉁불퉁한 그래프를 사용하게 되면 어느 지점에서 시작하는지에 따라 minimum이 달라집니다.
이런 지점은 local minimum이라고 합니다. 저희의 목표는 global minimum을 찾아야 합니다.
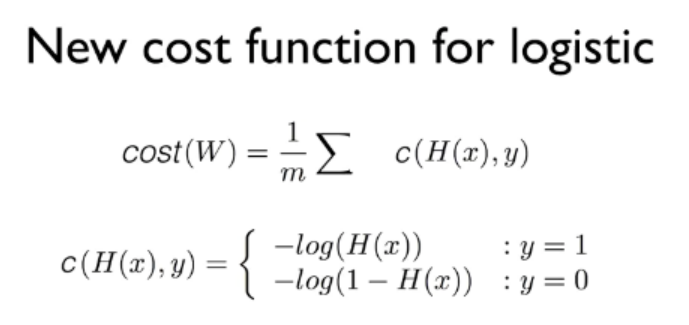
새로운 Cost 함수입니다. Cost 함수의 목적은 비용(cost)을 판단해서 올바른 W와 b를 찾는 것입니다. 다시 말해, 목표로 하는 W와 b를 찾을 수 있다면, 어떤 형태가 됐건 cost 함수라고 부를 수 있다는 뜻입니다.
log(로그)를 사용하는 이유는 앞에서 잠깐 언급했던 것처럼, 구불구불한 cost 함수를 매끈하게 펴기 위함입니다. 당연히 첫 번째 목표는 hypothesis가 반영된 비용을 올바르게 판단하기 위함입니다.
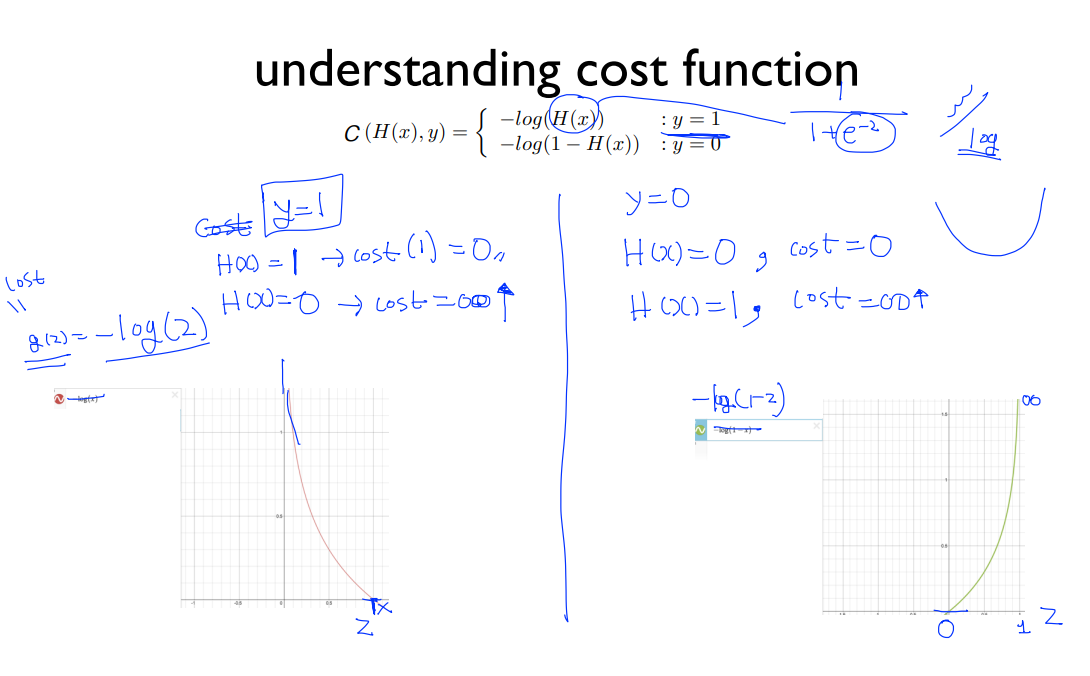
아래쪽에 그래프가 2개 있습니다. 매끈한 밥그릇의 왼쪽을 담당하는 그래프와 오른쪽을 담당하는 그래프. 두 개를 합쳐서 하나의 밥그릇을 만듭니다. log 함수가 매끈하기 때문에 gradient descent 또한 잘 동작한다.
왼쪽은 -log(z)의 그래프이고, 오른쪽은 -log(1-z)의 그래프입니다.
교수님께서 y 값이 1일 때와 0일 때에 대해 손수 적어놓으셨다. 한번 따라가 보자.
y가 1일 때 H(X) = 1일 때는 왼쪽 그래프에서 y는 0이 된다. (cost=0)
H(X) = 0일 때는 왼쪽 그래프에서 y는 무한대(∞)가 된다. (cost=무한대)
y가 0일 때 H(X) = 0일 때는 오른쪽 그래프에서 y는 0이 된다. (cost=0)
H(X) = 1일 때는 오른쪽 그래프에서 y는 무한대가 된다. (cost=무한대)
y는 파일 등에서 가져온 실제 데이터(label)이고, H(X)는 y를 예측한 값(y hat)이다.
그래서, H(X)는 기존의 hypothesis처럼 틀릴 수 있는 가능성이 있다.
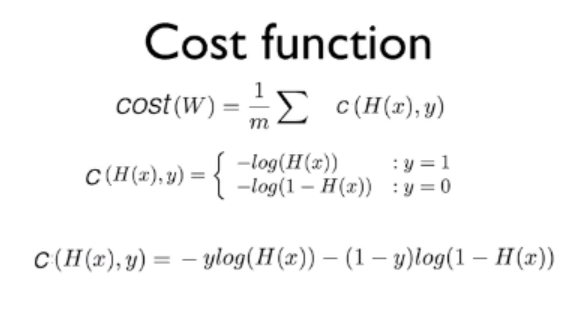
마지막 공식은 가운데 있는 공식을 하나로 합친 공식입니다.
하나로 만들지 않으면, 코딩할 때마다 조건문이 들어가기 때문에 불편합니다.
아주 간단한 공식입니다. y에 대해 1 또는 0을 넣어보면 원하는 값만 사용할 수 있음을 쉽게 알 수 있습니다.
2.2 Minimize cost - Gradient descent algorithm

Cost를 minimize를 하기 위해서 Gradient descent algorithm(경사 하강법)을 사용합니다.
앞에서 만들었던 공식을 cost 함수와 합쳤습니다.
일단 아래처럼 음수 기호(-)를 앞으로 빼서 안쪽을 +로 만듭니다.
-ylog(H(x)) - (1-y) log(1-H(x)) ==> -(ylog(H(x)) + (1-y) log(1-H(x)))
cost 함수인 cost(W) = (1/m) ∑ c(H(x), y)를 재구성합니다.
(1/m) ∑ -(ylog(H(x)) + (1-y) log(1-H(x))) ==> -(1/m) ∑ylog(H(x)) + (1-y) log(1-H(x))
두 번째 있는 공식은 cost(W)에 대해 미분을 적용해서 W의 다음번 위치를 계산하는 공식입니다.
Linear Regression과 공식에서는 달라진 게 없지만, 김성훈 교수님께서 말씀하신 것처럼 cost(W)가 달라져서 매우 복잡한 미분이 되어 버렸습니다.
강좌에서도 이 부분을 생략하셨기 때문에, 우리 또한 "미분을 하는구나!" 정도로 넘어가야 하는 부분입니다.
'Main > Machine Learning' 카테고리의 다른 글
| [ML - lec 07] ML의 실용과 몇 가지 팁 (0) | 2022.03.13 |
|---|---|
| [ML - lec 06] Softmax Regression (Multinomial Logistic Regression) (0) | 2022.03.13 |
| [ML - lec 04] Multi-variable linear regression (0) | 2022.03.06 |
| [ML - lec 02,03] Linear Regression의 Hypothesis와 cost (0) | 2022.03.06 |
| [ML-분류] 앙상블 학습(Ensemble Learning) (0) | 2022.02.04 |




댓글