본 내용은 김성훈 교수님의 '모두를 위한 딥러닝 시즌1' 강의와
https://pythonkim.tistory.com/notice/25를 참고하여 제작하였습니다.
목차
1. Softmax Regression 기본 개념 소개
1.1 Logistic (regression) classification

지난 Chapter에서 Logistic regression에 대해서 학습했었습니다.
기본적으로 출발은 linear 한 방정식으로 시작을 합니다.
하지만 단점이 있었습니다. 해당 방정식으로는 binary classification 즉, 0이냐 1이냐를 고르는 문제를 해결하기에 적합하지 않았습니다.
따라서, 큰값을 압축하여 0이나 1 사이 값으로 나와주도록 하는 새로운 함수가 필요했습니다.
많은 사람들이 연구 끝에 찾아낸 함수를 Sigmoid(시그모이드) 또는 Logistic(로지스틱) 이라고 부릅니다.

Logistic regression을 직관적으로 살펴보겠습니다.
Logistic classification을 학습시킨다는 것이 무엇이냐 함은 좌표상에 표현된 2개의 그룹을 나누는 직선(decision boundary)을 찾아내는 것입니다.
1.2 Multinomial classification

Logistic classification을 학습시킬 때의 아이디어를 그대로 multinomial classification에서도 적용할 수 있습니다.
여러 개의 label을 갖는 multinomial classification을 어떻게 구현할 수 있는지 보여주는 그림입니다.
좌표상에 A, B, C의 3개의 그룹이 있고, 오른쪽 그림에서 binary classification에서 사용한 decision boundary를 여러 개 그려놓았습니다.

이처럼 여러 개로 분류를 하기 위해서는 그림 오른쪽에 있는 것처럼 여러 개의 binary classification이 필요합니다.
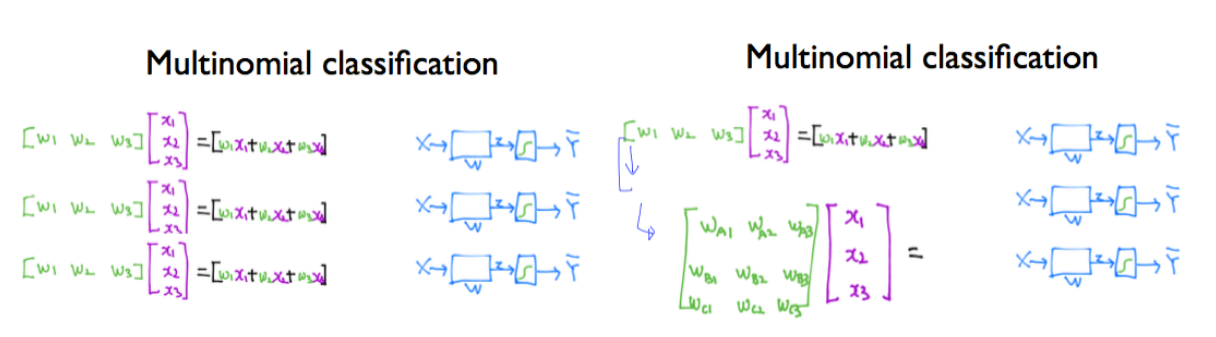
binary classification을 구현하려면, 그림 왼쪽에 있는 것처럼 각각 행렬 1개씩을 요구합니다.
3개의 binary classification이 필요하기 때문이죠.
하지만, 이렇게 독립적으로 구성되어 있으면 구현과 계산하기에 복잡합니다.
그래서 오른쪽 그림처럼 하나로 합쳐 계산을 진행할 수 있습니다.
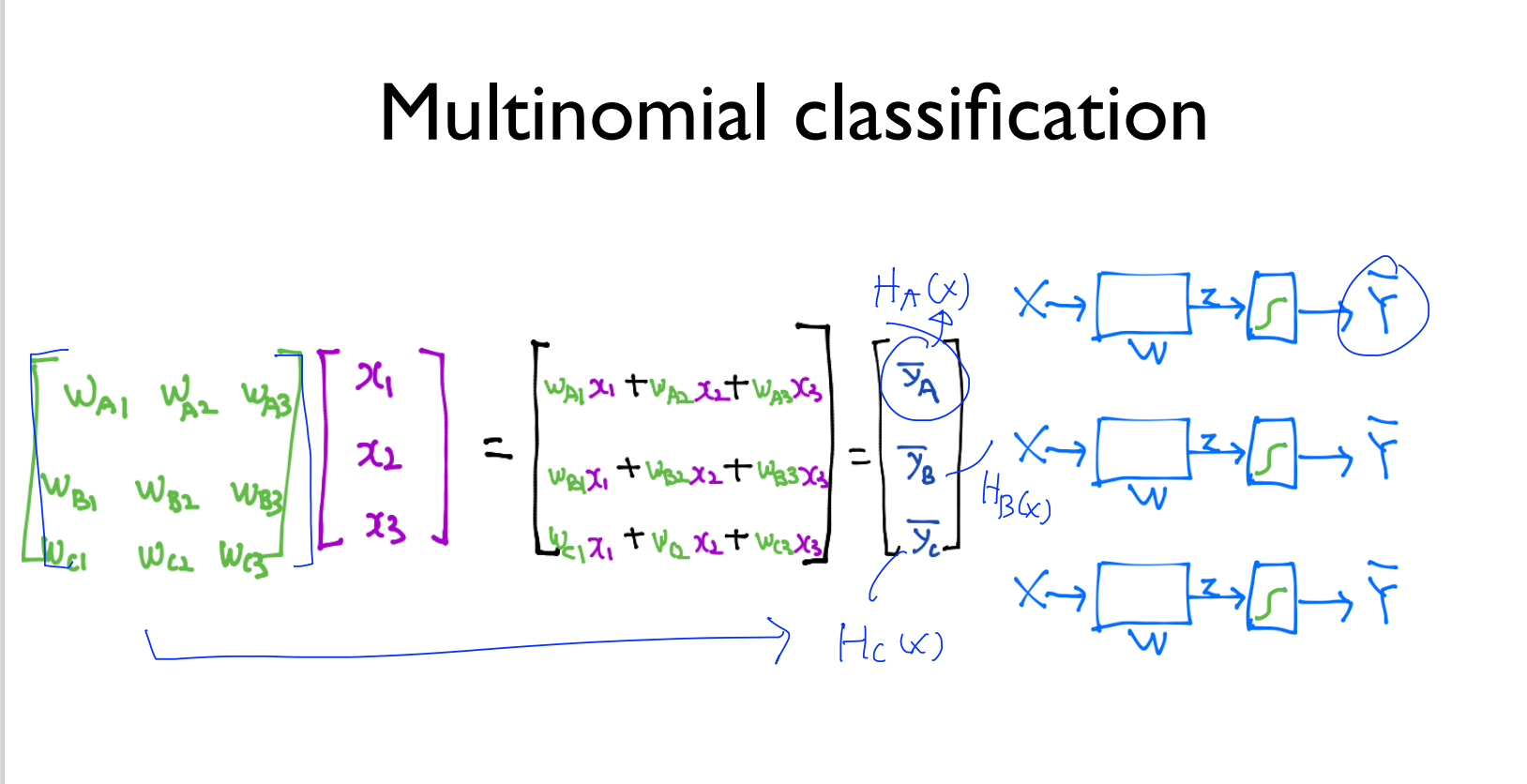
행렬 곱셉을 보여주고 있습니다.
결과적으로 행렬 곱셉의 결과는 3행 1열의 행렬이 만들어지게 되었고,
한 번에 계산이 되어 3개의 독립된 Classification처럼 동작을 하게 됩니다. 조금 더 간편해졌죠?
1.3 Sigmoid

그림 중간에 빨간색으로 표시된 2.0, 1.0, 0.1이 예측된 Y의 값입니다.
이 값을 W에 X를 곱하기 때문에 굉장히 크거나 작은 값일 수 있습니다.
그래서, 이 부분 뒤쪽에 sigmoid가 들어가서 값을 0과 1 사이로 조정하게 됩니다.
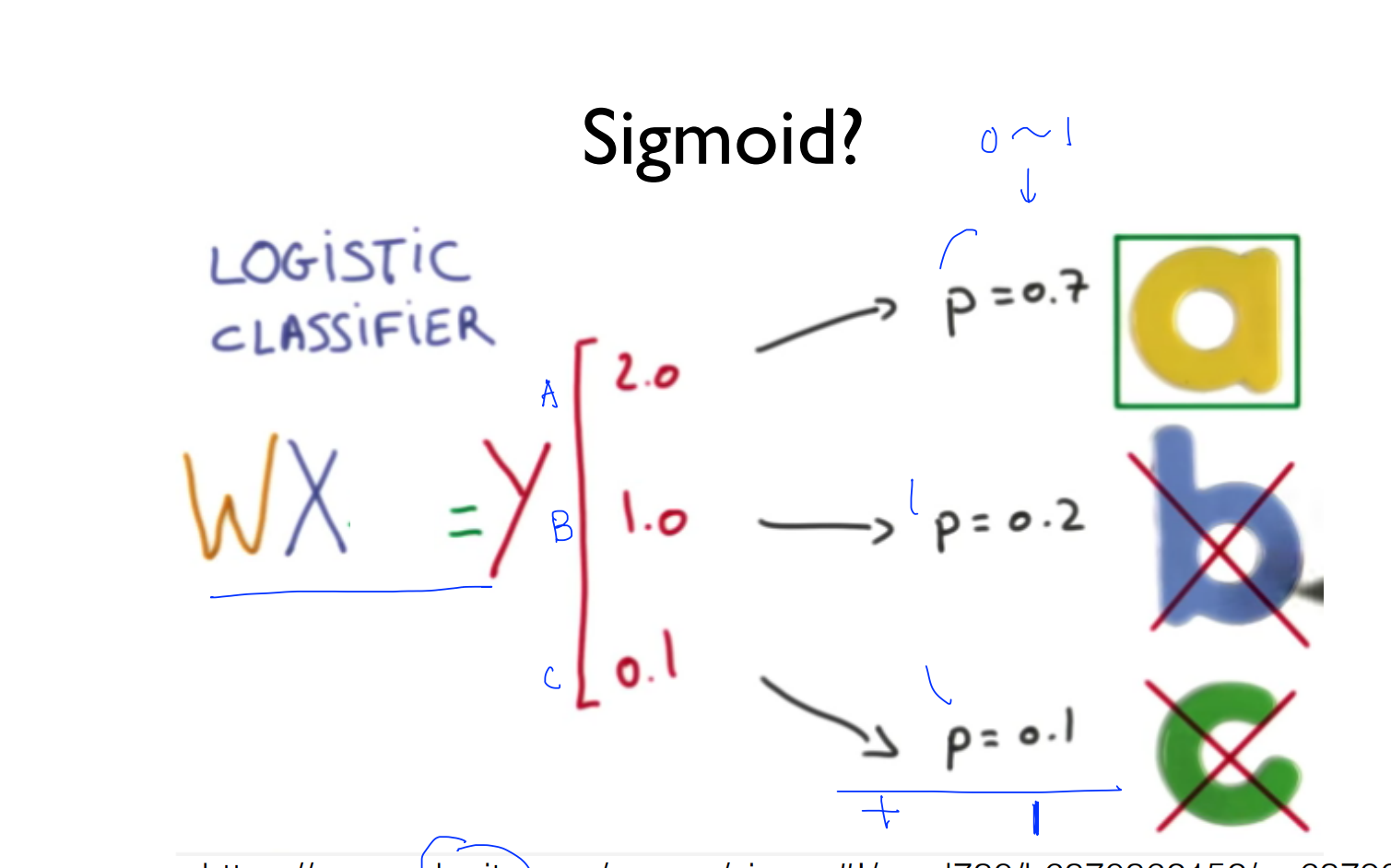
이 값들을 0과 1사이의 값으로 바꾸니까, 각각 0.7, 0.2, 0.1이 됐습니다.
이들을 모두 더하면 1이 됩니다. 따라서, a, b, c 중에서 하나를 고르자면 a를 선택하게 됩니다.
1.4 Softmax
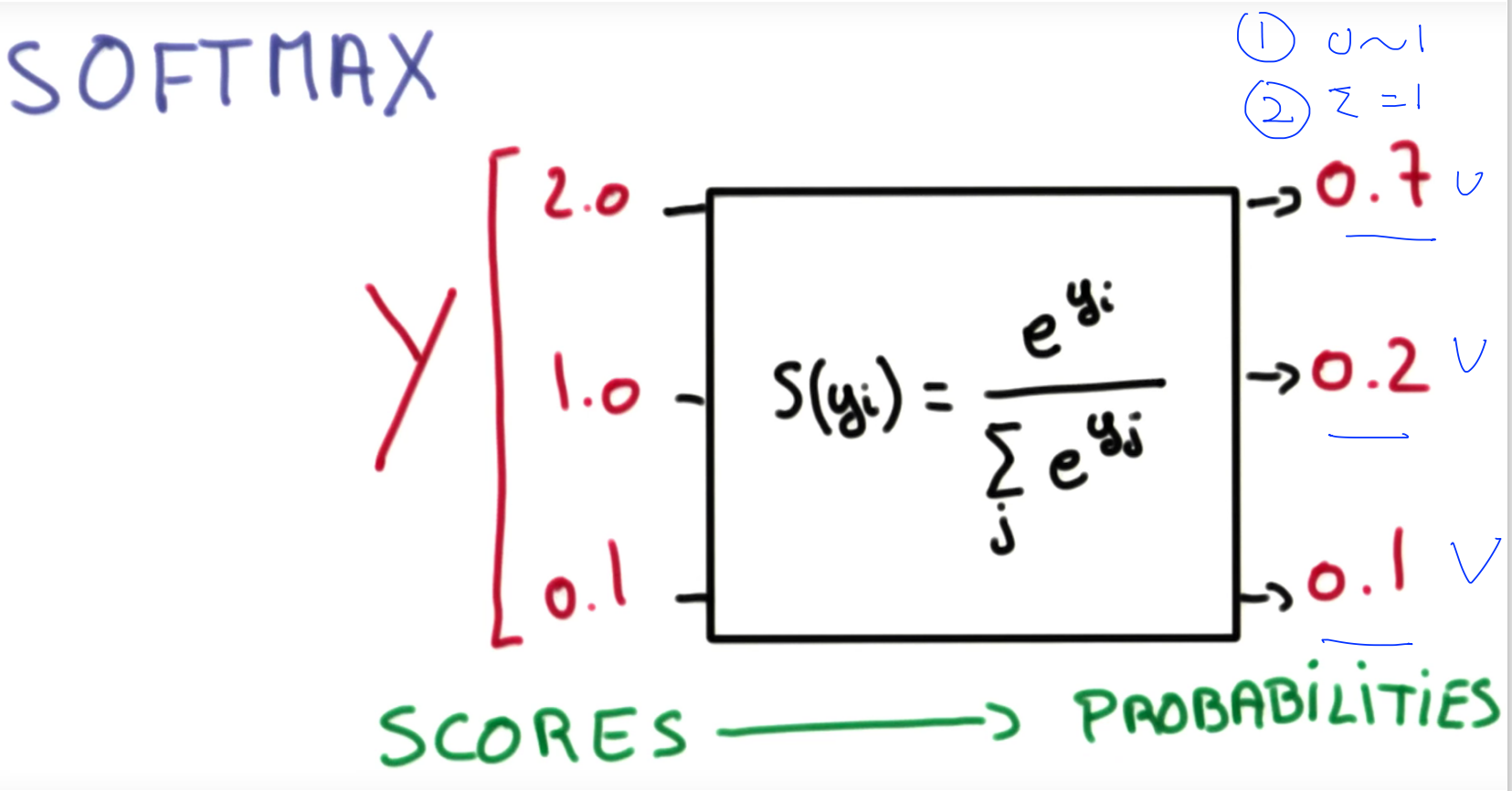
N개의 값을 Softmax에 넣게되면 우리가 원하는 것들이 다 들어가 있습니다.
Softmax는 두 가지 역할을 수행합니다.
1. 입력을 sigmoid와 마찬가지로 0과 1 사이의 값으로 변환한다.
2. 변환된 결과에 대한 합계가 1이 되도록 만들어 준다.
전체를 더하면 1이 되기 때문에 확률이라고 부르면 의미가 더욱 분명해집니다.
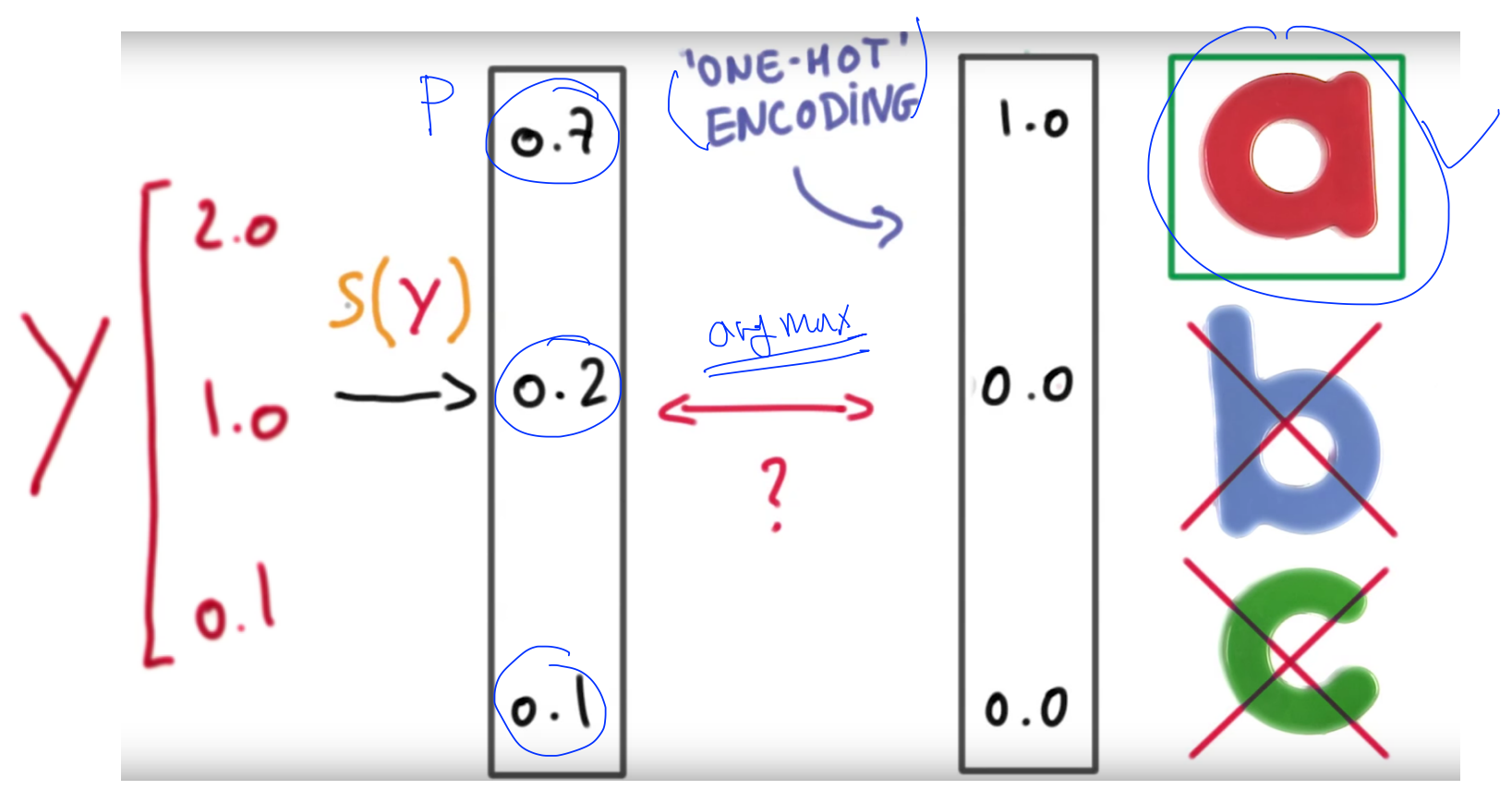
y를 예측한 이후부터의 과정을 알려주는 그림입니다.
one-hot encoding은 softmax로 구한 값 중에서 가장 큰 값을 1로, 나머지를 0으로 만듭니다.
1.5 Softmax vs Sigmoid
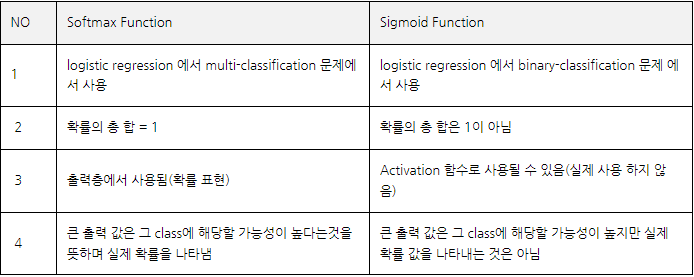
Softmax와 Sigmoid의 차이와 개념을 해당 표로 확인해보실 수 있습니다.
결론적으로
- sigmoid : binary-classification에서 사용
- softmax : multi-classification에서 사용
2. Softmax classifier의 cost함수
2.1 Cost function
지금까지의 과정을 통해 예측모델(Hypothesis)은 완성이 되었습니다.
그다음 단계로 예측 값과 실제 값이 얼마나 차이가 나는지를 나타내는 Cost function을 설계해야 합니다.
궁극적으로 Cost function을 최소화 함으로써 학습을 완성하게 됩니다.
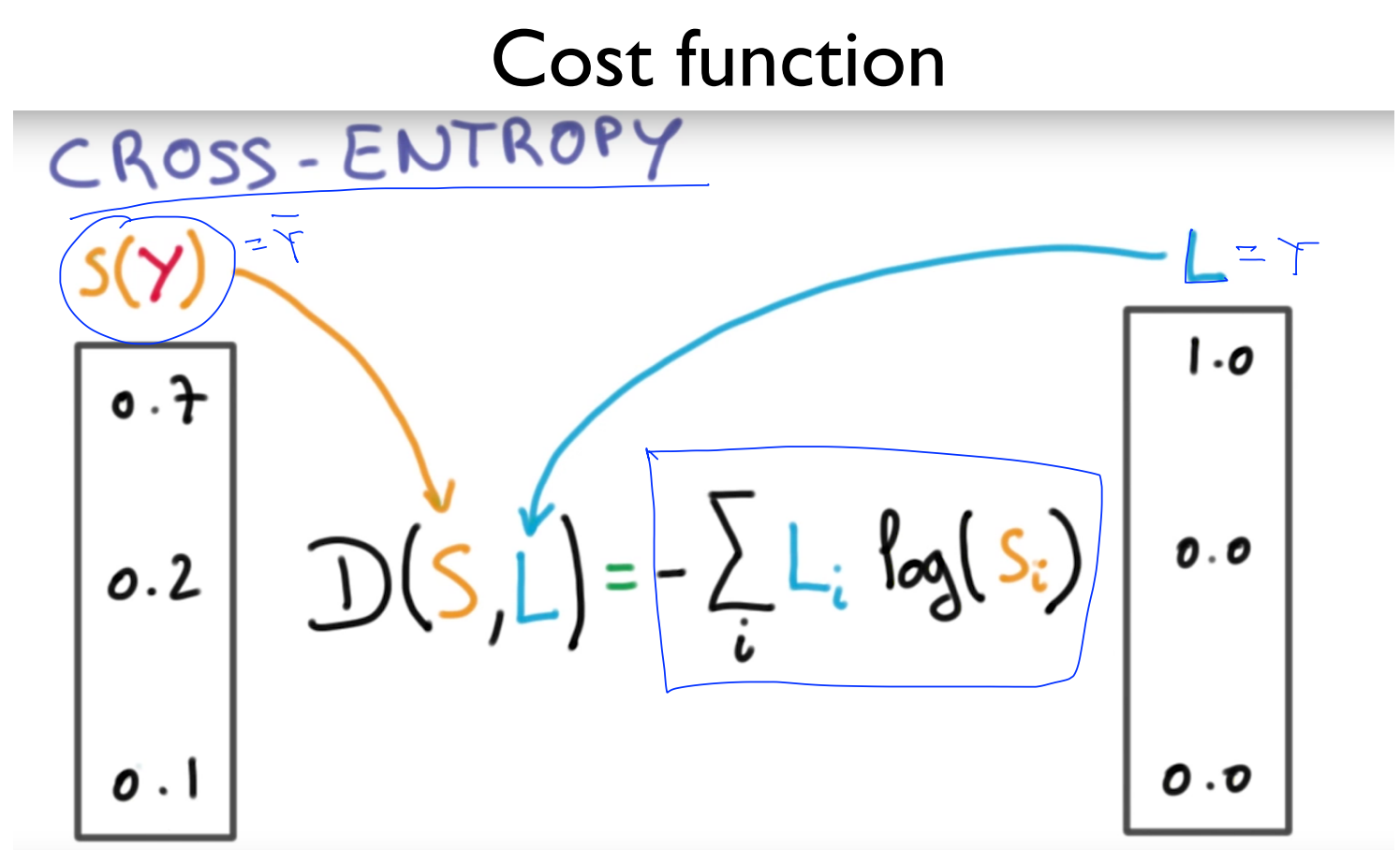
S(Y)는 softmax가 예측한 값이고, L(Y)는 실제 Y의 값으로 L은 label을 의미합니다. cost 함수는 예측한 값과 실제 값의 거리(distance, D)를 계산하는 함수로, 이 값이 줄어드는 방향으로, 즉 entropy가 감소하는 방향으로 진행하다 보면 최저점을 만나게 됩니다.
cross-entropy는 통계학 용어로, 두 확률 분포 p와 q 사이에 존재하는 정보량을 계산하는 방법을 말합니다.
왜 이 함수가 여기서 적합한 Cost function인지 살펴보도록 하겠습니다.
2.2 Cross-entropy cost function

Cross-entropy cost 함수가 제대로 동작한다는 것을 풀어서 설명하고 있습니다.
해당 Cost function을 각각의 element라고 생각하여 계산합시다.
-log함수는 지난 Chapter(Logistic regression)에서 본 적이 있을 겁니다. 오른쪽 그림에 표현되어 있습니다.
-log(~) 값은 softmax를 통한 값이기 때문에 항상 0~1 사이의 값을 가지게 됩니다.
해당 함수는 0일 때는 굉장히 커서 무한대에 가깝게 가고, 1일 때는 0이 되는 함수입니다.
자 이제 간단하게 하기 위해서 두 가지 label이 있다고 가정합시다.
L은 label의 약자로 Y의 실제 값입니다. Y hat은 Y를 예측한 값으로, 맞게 예측했을 때와 틀리게 예측했을 때를 보여주고 있습니다.
위의 공식이 A와 B 중에서 하나를 선택해야 한다면, 현재 L에 들어있는 값은 B에 해당하는 요소가 1이므로 B를 가리킵니다. 첫 번째 Y hat은 B를 가리키니까 맞게 예측했고, 두 번째 Y hat은 A를 가리키므로 잘못 예측했습니다.
element-wise 곱셈을 적용한 최종 결과를 보면, 맞게 예측했을 때는 0이 나오고, 잘못 예측했을 때는 무한대가 나왔습니다.
잘 동작하는 cost 함수임을 알 수 있습니다.
2.3 Logistic cost vs cross entropy

이전에 Logistic cost function을 다룰 때 이처럼 복잡한 형태를 다루었었죠?
사실상 저 형태가 cross entropy였습니다. 왜 같을까요?? 교수님께서는 해당 이유를 과제로 내주셨습니다.
많은 수강생들의 의견을 참고하여 이유들을 찾아보았습니다.
개념적인 이유:
cost 함수의 목적은 틀렸을 때 벌을 주어서 비용을 크게 만들어야 하는데, 양쪽 모두 무한대라는 벌칙을 적용합니다. 다만 Logistic regression에서는 2개의 log 식을 연결해서 사용하지만 cross-entropy에서는 행렬로 한 번에 계산하는 방식을 취할 뿐입니다. 즉, Logistic regression을 cross-entropy로 처리할 수 있습니다.
바로 앞에 나온 2개 중에 하나를 선택하는 그림이 Logistoic regression의 cross-entropy 버전입니다.
cross entropy 하나로 Logistoic regression까지 처리할 수 있으므로, 포함 관계로 생각할 수도 있을 것 같습니다.
수식적인 이유:
두 함수가 같은 이유는 두 개의 예측 및 결과만 있기에 -시그마(Li * log(Si) = -(L1*log(S1))-(L2*log(S2))입니다.
실제 값 L1, L2은 1과 0, 그리고 서로 반대의 값을 지닐 수밖에 없기 때문에 L2 = 1-L1 일 수밖에 없습니다. (0 또는 1, 1 또는 0)
S1, S2은 예측값이기 때문에 1,0 만 나오는 것은 아니지만 둘의 합은 1이 될 수밖에 없습니다. (0.3, 0.7 등 그러나 어쨌든 1-L0 = L1)
따라서 -L1*log(S1)-(1-L1)*log(1-S1)가 됩니다.
L1 = y, S1 = H(x)로 바꾸면 -y*log(H(x))-(1-y)*log(1-H(x))가 되는 것입니다.
2.4 Gradient descent
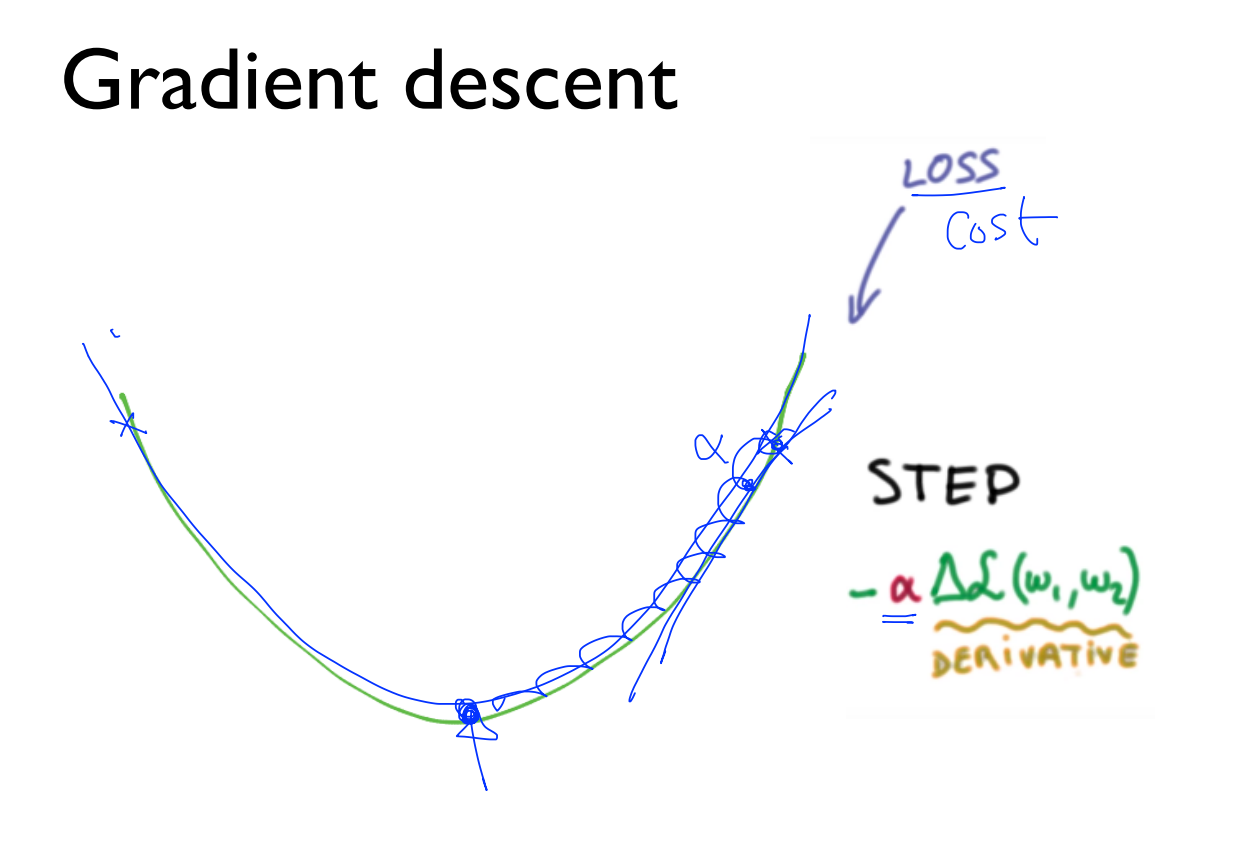
Cross-entropy cost function를 만들었다면, Gradient descent 알고리즘에 적용해서 최소 비용을 찾아야 합니다. 역시 이때 중요한 것은 그림에 표현된 w1, w2의 값입니다. 알파(a)는 learning rate로 어느 정도로 이동할 것인지를 알려주고, 알파 오른쪽의 삼각형은 미분을 한다는 뜻입니다.
미분하는 것은 너무 복잡하기 때문에 생략하도록 하겠습니다.
'Main > Machine Learning' 카테고리의 다른 글
| [ML - lec 07] ML의 실용과 몇 가지 팁 (0) | 2022.03.13 |
|---|---|
| [ML - lec 05] Logistic (Regression) Classification (0) | 2022.03.06 |
| [ML - lec 04] Multi-variable linear regression (0) | 2022.03.06 |
| [ML - lec 02,03] Linear Regression의 Hypothesis와 cost (0) | 2022.03.06 |
| [ML-분류] 앙상블 학습(Ensemble Learning) (0) | 2022.02.04 |




댓글